1.6. Погрешность счислимого места и вероятностная оценка точности счисления
При отсутствии непрерывныхобсерваций, получаемых с помощью КНС или РНС, основой решения задачи обеспечения навигационной безопасности плавания является счисление пути, позволяющее непрерывно и на любой заданный момент времени определять координаты корабля. Обсервации производятся эпизодически и предназначаются для коррекции счисления. В общем случае все расчеты по оценке навигационной безопасности в открытом море опираются на информацию о счислимом месте корабля.
Известно [13], что средняя квадратическая погрешность счислимого места квадратически складывается из СКП последней обсервации Мо и из СКП счисления Мс (t)
![]() (1.6.1)
(1.6.1)
Поэтому анализ точности счислимого места, производимый для оценки навигационной безопасности плавания, начинается с оценки точности счисления.
Счисление ведется по показаниям автономных технических средств морской навигации с учетом внешних факторов, воздействующих на движение корабля, – течения и дрейфа. Следовательно, на точность плавания по счислению оказывают влияние погрешности определения курса, относительной скорости, вектора скорости течения и угла дрейфа.
Погрешности современных отрегулированных гироскопических курсоуказателей и лагов, как правило, незначительны. Тем более малыми являются погрешности навигационных инерциальных комплексов. При плавании с учетом информации только от относительных лагов или с периодическим включением абсолютного лага главным фактором, формирующим погрешность счисления, является неточное знание элементов течения, обусловленное их случайной изменчивостью во времени и в пространстве.
Среднюю квадратическую погрешность счисления можно оценивать тремя способами: способом, основанным на обработке невязок счисления (по статистическим параметрам точности счисления), по погрешностям элементов счисления и по параметрам автокорреляционных функций течения и средств счисления.
Первый из этих способов в настоящее время является основным, так как он основан на использовании таких статистических величин, которые являются следствием всех факторов, влияющих на точность счисления, и которые могут быть получены в результате практического плавания кораблей без привлечения результатов исследования океанографических характеристик Мирового океана.
Оценка случайной погрешности счисления
по статистике невязок
Для оценки точности плавания кораблей по счислению в настоящее время широко используется вероятностная модель погрешностей, опирающаяся на статистику невязок. При сравнительно точных обсервациях модули невязок являются следствием случайных погрешностей счисления.
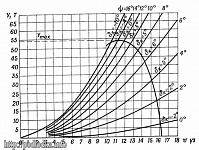
В научно-исследовательских работах, проводимых в ГосНИНГИ в рамках обобщения опыта точности плавания кораблей в различных районах Мирового океана, а также в руководствах и методиках [39, 32, 42], показано, что радиальная средняя квадратическая погреш![]() ность счисления Мс (t) зависит от интервала счисления t и характеризуется двумя параметрами точности счисления – коэффициентом точности счисления Кс и величиной q, определяющей степень нелинейности функции Мс (t):
ность счисления Мс (t) зависит от интервала счисления t и характеризуется двумя параметрами точности счисления – коэффициентом точности счисления Кс и величиной q, определяющей степень нелинейности функции Мс (t):

![]()
![]()
![]() (1.6.2)
(1.6.2)
Данная модель получена опытным путем в результате обработки фактических данных о точности плавания кораблей и судов. Она составлена в предположении того, что линейное нарастание радиальных погрешностей счисления соответствует интервалу tл, равному примерно двум часам. При интервалах счисления t > 2 ч радиальная погрешность счисления изменяется по нелинейному закону.
В реальных условиях параметр tл может принимать значения, существенно отличающиеся от вышеуказанных. Поэтому величина tл является третьим параметром точности счисления. В методике [32] приведены интервалы линейного нарастания погрешности счисления, находящиеся в пределах от 2 ч (при плавании в районах с существенно преобладающей случайно изменяющейся переменной составляющей) до 10 ч (в районах с существенно преобладающей постоянной составляющей). Примерно такие же значения параметра tл приведены и в статье [4], но здесь они поставлены в зависимость от скорости корабля.
Следовательно, модель (1.6.2) с параметром tл = 2 ч может оказаться слишком приближенной, неадекватной реальным условиям.
Обобщенные результаты обработки фактических данных, полученные в ГосНИНГИ, а также информация, приведенная в [32], свидетельствуют о том, что параметр q в зависимости от характера течения находится в пределах 0,3 £ q £ 0,8.
Для получения формулы, учитывающей различные возможные значения параметров tл и q, рассмотрим зависимости, определяющие общий характер изменения радиальной СКП счисления на линейном и нелинейном участках графика Мс (t):
 (1.6.3)
(1.6.3)
где К – коэффициент, характеризующий скорость линейного нарастания радиальной СКП счисления на интервале tл.
Для граничного интервала точности счисления t = tл справедливо равенство Кtл = Ксtлq. Отсюда
К = Ксtлq-1. (1.6.4)
Подставив это выражение в первую формулу выражения (1.6.2), будем иметь обобщенную модель радиальной СКП счисления, учитывающую все три параметра точности счисления (Кс, q и tл):
 (1.6.5)
(1.6.5)
В этих формулах Мс (t) выражена в милях, t – в часах, а размерность Кс в обеих формулах одинаковая – [мили / чq].
Наиболее часто используемые в настоящее время формулы [2, 13, 39, 42]
 (1.6.6)
(1.6.6)
выведенные для параметров tл = 2 ч и q = 0,5, являются частным случаем обобщенных формул (1.6.5).
При плавании без учета течения величина Кс зависит, главным образом, от района плавания и от сезона года.
При плавании с учетом течения коэффициент точности счисления зависит от точности и частоты определения вектора скорости течения. Чем точнее средства и методы определения течения, учитываемого при счислении, и чем чаще оно определяется, тем меньше коэффициент точности счисления и, следовательно, тем точнее плавание по счислению. Отсюда следует, что плавание с использованием современных навигационных комплексов, непрерывно или дискретно вырабатывающих вектор абсолютной скорости корабля, существенно точнее, чем плавание с обычными средствами курсоуказания и скорости.
Наиболее вероятным при плавании в открытом море параметрам q = 0,5 и tл = 2 … 4 ч соответствуют коэффициенты точности счисления, находящиеся в следующих ориентировочных пределах:
– при плавании без учета течения – 1,6 … 3,0;
– при плавании с использованием информации о скорости корабля только от относительного лага и с учетом течения, выбранного из навигационных пособий, – 1,0 … 2,0;
– при плавании с использованием информации о скорости корабля только от относительного лага и при определении течения по высокоточным обсервациям (с периодичностью 1 … 2 ч) – 0,8 … 1,6;
– при плавании с использованием навигационного комплекса с инерциальной навигационной системой (ИНС) при дискретном определении течения по показаниям абсолютного и относительного лагов (через каждые 0,5 … 1,5 ч) – 0,4 … 0,6;
– при плавании с использованием навигационного комплекса с инерциальной навигационной системой и при непрерывной работе абсолютного лага – 0,1 … 0,3.
При океанском плавании с относительным лагом в штормовых условиях по данным учебника [2] коэффициент точности счисления может достигать величины 3,0 … 4,0.
Наиболее достоверно все параметры точности счисления Кс, q и tл определяются комплексно по результатам статистической обработки модулей невязок, полученных по высокоточным обсервациям при плавании в данном море с использованием одного и того же режима работы навигационного комплекса и одного и того же метода оценки вектора скорости течения. Для осреднения пространственной и временной корреляции элементов течения, при определении параметров точности счисления используются невязки, полученные на различных курсах и скоростях кораблей.
Методика комплексного расчета параметров точности счисления Кс и q (для заданного значения tл) изложена в ряде пособий (см., например, [14]). В работах [4, 5, 15] приводится методика расчета коэффициента точности счисления, основанная на использовании параметров автокорреляционной функции морского течения.
Важно иметь в виду, что при использовании навигационного комплекса с ИНС случайная погрешность широты практически не зависит от интервала счисления и для данного режима работы комплекса принимается величиной постоянной, которая определяется по данным, характеризующим работу системы. В этом случае параметры точности счисления определяются по проекциям невязок на параллель и используются только для оценки точности плавания по долготе.
Поскольку условия данного плавания, как правило, отличаются от осредненных условий, при которых определялись параметры точности счисления, то последние могут использоваться лишь для ориентировочного прогнозирования точности плавания по счислению в заданном районе.
Оценка точности счисления
по погрешностям элементов счисления
Для анализа навигационной безопасности плавания непосредственно в море на интервалах счисления, не выходящих за пределы линейного участка нарастания СКП счисления, целесообразно использовать прямой способ оценки точности счисления, основанный на учете текущих погрешностей элементов счисления и не зависящий от статистических параметров точности счисления.
В этом случае после каждого определения вектора скорости течения (по обсервации или по показаниям абсолютного и относительного лагов) рассчитываются средние квадратические погрешности элементов выявленного сноса и затем вычисляется радиальная СКП счисления:
 (1.6.7)
(1.6.7)
В этой формуле m – средняя квадратическая погрешность того элемента счисления, который обозначен в индексе данного символа.
СКП элементов течения вычисляются способами, зависящими от средств и методов определения течения [13, 42]. СКП направления линии истинного курса квадратически складывается из СКП курсоуказателя (определяется по формуляру курсоуказателя) и из СКП его поправки. СКП относительной скорости определяется по результатам ее последних замеров на мерном полигоне.
Поскольку главный вклад в погрешность счисления вносит неточное знание элементов течения, то при отсутствии достоверных данных о погрешностях систем курсоуказания и относительной скорости радиальная СКП счисления может быть приближенно рассчитана по двум последним слагаемым, стоящим под знаком корня.
Существенным достоинством способа оценки точности счисления по погрешностям элементов счисления являются три фактора: исключается необходимость накопления совокупности невязок и, следовательно, способ применим в неоплаванных районах; способ реагирует на изменяющиеся условия плавания (так как учитываются реальные погрешности оценки элементов течения, зависящие от способа определения течения); простота способа. К недостатку способа следует отнести ограниченность его использования пределами линейного нарастания СКП счисления.
Оценка случайной погрешности счисления по параметрам
автокорреляционных функций течения и средств счисления
Радиальная средняя квадратическая погрешность счисления Мс (t) является функцией векториальных средних квадратических погрешностей учитываемых течения, дрейфа, курса и относительной скорости. Для простоты примем взаимно перпендикулярные проекции (на меридиан и параллель) каждой из указанных векториальных СКП одинаковыми и обозначим их символами sc1(t), sc2(t), sc3(t) и sc4(t), соответственно. Тогда получим
![]() (1.6.8)
(1.6.8)
Средняя квадратическая погрешность счисления sc1(t), обусловленная неточностью учитываемого вектора скорости течения.
Неточное знание течения является основным фактором, формирующим погрешность счисления.
Физическая природа морских течений такова, что они обладают значительной случайной изменчивостью во времени и в пространстве. Поэтому элементы течения, определенные в данный момент и в данной точке, могут существенным образом отличаться от их значений, определенных в другой момент или в другой точке.
Случайность непериодического течения предопределяет вероятностный характер его оценки на моменты времени, не совпадающие с моментом измерения направления и скорости течения. Для этого используется математический аппарат теории случайных функций.
Основой этого аппарата являются автокорреляционные функции, устанавливающие вероятностную взаимосвязь между скоростями течения в различные моменты времени (в различных точках пространства) и позволяющие прогнозировать вероятнейшие значения скорости течения. При анализе морских течений вектор скорости течения чаще всего раскладывают на две составляющие (по географическим координатным осям).
Поскольку средние квадратические значения каждой составляющей приняты одинаковыми, то в дальнейшем речь будет идти об одной проекции sс1 средней квадратической погрешности счисления, а оценка радиальной погрешности счисления за счет неточности течения будет производиться с учетом обеих составляющих.
В скорости морского течения выделяют две составляющие: низкочастотную, или долгопериодную, и высокочастотную, или короткопериодную.
Низкочастотная составляющая изменяется медленно. Средний период ее изменения может измеряться десятками часов или даже сутками. Поэтому низкочастотная составляющая при решении задач навигационной безопасности принимается за квазипостоянное (как бы постоянное) течение для данного короткого периода плавания между измерениями течения или между обсервациями.
Высокочастотная составляющая течения более подвижна и изменчива. Период ее изменения для большинства открытых районов океана составляет всего несколько часов. Высокочастотную составляющую течения называют переменным течением.
Автокорреляционные функции низкочастотной и высокочастотной составляющих течения открытого моря чаще всего аппроксимируются уравнениями следующего вида:
 (1.6.9)
(1.6.9)
В этой формуле s2 – дисперсия скорости течения (его одной составляющей); a и b – параметры автокорреляционной функции, первый из них характеризует степень затухания корреляционной связи, второй – «колебательность» корреляционной функции относительно оси времени (соответствует преобладающей частоте в спектре случайного процесса).
Дисперсию квазипостоянной составляющей скорости течения будем обозначать s2п, дисперсию переменной составляющей – s2пр. Также: aп – параметр квазипостоянной составляющей скорости течения, aпр – параметр переменной составляющей.
Вид и параметры автокорреляционной функции определяются опытным путем по результатам многочисленных замеров проекций скорости течения в данном ограниченном районе моря.
По данным работ [4, 5], в открытых районах Мирового океана автокорреляционная функция проекций скорости течения аппроксимируется первой формулой (1.6.9), а обобщенные среднестатистические характеристики ее параметров s2 и a, вычисленные по длительным (месячным) измерениям течений, приведены в табл. 1.6.1 (в этой таблице V – скорость корабля в узлах). Эти данные опубликованы в статье [4].
В ограниченных районах океана и в отдельных морях вид и параметры автокорреляционной функции могут существенно отличаться от указанных в этой таблице.
Т а б л и ц а 1.6.1
| Вид течения (составляющие течения) | Параметры | |
| s2 | a | |
| Квазипостоянное Переменное | s2п = 0,12 уз2 s2пр = 0,20 уз2 | aп = 0,02V ч–1 aпр = 0,1+(V / 10)2/3 ч–1 |
Скорость корабля, обусловленная воздействием течения, так же, как и само течение, изменяется случайным образом, но характер случайной функции изменения скорости корабля будет несколько сглаженным. Степень сглаживающего эффекта зависит от инерционных и гидродинамических характеристик корабля. С точностью, достаточной для оценочных характеристик погрешностей счисления, можно принять, что автокорреляционная функция изменения скорости корабля под воздействием течения имеет такие же параметры, как и автокорреляционная функция скорости течения.
Случайные колебания скорости корабля, обусловленные воздействием течения, вызывают накапливающуюся с течением времени случайную погрешность счисления, которая на определенном интервале времени может быть принята за стационарную случайную функцию. Поскольку автокорреляционная функция случайной погрешности счисления приближенно соответствует автокорреляционной функции течения, то на основании правила о дисперсии интеграла стационарной случайной функции [44], дисперсия счисления выражается формулой, учитывающей воздействия на корабль всех составляющих скорости морского течения:
 (1.6.10)
(1.6.10)
где t – время плавания по счислению, ч; Кп (t) и Кпр (t) – автокорреляционные функции квазипостоянной и переменной составляющих скорости течения соответственно [вид этих функций определяется формулами (1.6.9)]; sд – среднее квадратическое значение скорости ветрового (дрейфового) течения в узлах, обусловленного воздействием на водную поверхность силы ветра.
В приповерхностном слое, то есть на глубине до 20 м, величина sд в узлах вычисляется по приближенной формуле [32]: sд = =0,12 + 0,02u, где u – скорость устоявшегося истинного ветра в м/с. Скорость ветрового течения уменьшается с глубиной: на глубине 60 м оно составляет 0,4sд, а на глубине 100 м – 0,2sд. На глубинах свыше 100 м ветровое течение практически отсутствует.
В табл. 1.6.2 представлены вычисленные по этой формуле средние квадратические погрешности счисления sс1(t) в милях, соответствующие плаванию без учета течения и с нулевым значением ветровой составляющей. Таблица рассчитана по автокорреляционной функции усредненного океанского течения [4] [с учетом первой формулы (1.6.9) и параметров, указанных в табл. 1.6.1].
Произведя по этим табличным данным расчеты радиальной СКП счисления (она в 1,4 раза больше линейной СКП одной проекции, указанной в таблице), обнаружится, что при суточном плавании в океане со средней скоростью 10 уз без учета течения радиальная СКП счисления составит около 8 миль, а при плавании со скоростями 15 … 20 уз – в пределах 6 …7 миль. Ошибка счисления нарастает в среднем на 0,3 мили за каждый час плавания.
При рассматриваемых параметрах автокорреляционных функций с увеличением скорости погрешность счисления, обусловленная неучетом океанского течения, уменьшается. Так, например, разница в погрешностях счисления при суточном плавании скоростями 5 и 25 уз составляет 3 мили, то есть СКП счисления на скорости 25 уз меньше СКП при плавании со скоростью 5 уз в 1,8 раза.
Т а б л и ц а 1.6.2
| Интервал счиcления, ч | Скорость судна, уз | ||||
| 5 | 10 | 15 | 20 | 25 | |
| 0,2 0,4 0,6 0,8 1,0 1,4 1,6 2,0 6,0 10,0 14,0 18,0 22,0 24,0 | 0,11 0,22 0,32 0,42 0,52 0,71 0,81 0,98 2,47 3,68 4,73 5,67 6,53 6,93 | 0,11 0,21 0,31 0,41 0,51 0,68 0,76 0,92 2,20 3,18 3,99 4,68 5,30 5,58 | 0,11 0,21 0,31 0,40 0,49 0,65 0,73 0,88 2,02 2,84 3,51 4,08 4,57 4,80 | 0,11 0,21 0,30 0,39 0,48 0,63 0,70 0,84 1,87 2,60 3,17 3,66 4,09 4,29 | 0,11 0,21 0,30 0,38 0,46 0,61 0,68 0,81 1,76 2,41 2,92 3,35 3,74 3,92 |
При плавании с учетом выявленного течения ошибка счисления уменьшается. В первоначальный период после определения течения она практически равна нулю (если не учитывать погрешности способа определения течения). Но поскольку характер случайной изменчивости течения остается прежним, то в последующем в выявленном и учитываемом течении появляются погрешности. Это значит, что учитываемое течение, изменяясь со временем, будет устаревать. Следовательно, с увеличением времени, прошедшего после определения течения, будет увеличиваться и погрешность счисления.
Прогнозируемые значения средних квадратических погрешностей квазипостоянной (![]() ) и переменной (
) и переменной (![]() ) составляющих учитываемых проекций скорости течения через интервал времени t после определения течения рассчитываются по формулам [24]:
) составляющих учитываемых проекций скорости течения через интервал времени t после определения течения рассчитываются по формулам [24]:
 (1.6.11)
(1.6.11)
где rп (t) и rпр (t) – нормированные автокорреляционные функции квазипостоянного и переменного течений (соответственно), равные частному от деления соответствующих автокорреляционных функций на квадраты их средних квадратических погрешностей.
Квадрат радиальной СКП счисления после определения скорости течения (без учета дрейфовой составляющей) для первой корреляционной функции (1.6.9) вычисляется по формуле, приведенной в работе [4]:

где i = 1 – индекс параметров, соответствующих квазипостоянной составляющей (см. табл. 1.6.1); i = 2 – индекс параметров, соответствующих переменной составляющей; N – количество измерений скорости течения; Dt – дискретность измерения течения.
Расчеты радиальной СКП счисления, выполненные по этой формуле (после извлечения корня) для 12-часового интервала плавания по счислению скоростью 15 уз и для различного количества измерений течения, приведены в табл. 1.6.3.
Линейная СКП счисления без учета течения на этом временном интервале в соответствии с табл. 1.6.2 составляет 3,2 мили, а радиальная СКП равна 4,5 мили. Отношение этого значения к радиальным СКП, указанными в табл. 1.6.3, определяет эффективность k учета течения (последний столбец таблицы). Две последних строки этой таблицы (k < 1) свидетельствуют о том, что длительный учет одного течения приводит к погрешностям счисления, превышающим те, которые были бы при плавании без учета течения.
Т а б л и ц а 1.6.3
| N | Dt, ч | Мc (t), мили | k |
| 12 6 4 3 2 1 | 4 2 3 4 6 12 | 1,2 2,4 3,4 4,3 5,8 9,3 | 3,8 1,9 1,3 1,0 0,8 0,5 |
Расчеты для рассматриваемой корреляционной функции показывают, что оптимальная (по критерию точности счисления) длительность учета последнего измеренного течения при скорости корабля 5 уз составляет 1,8 ч. Чем больше скорость корабля, тем больше влияние пространственной изменчивости течения, поэтому длительность учета течения при скорости корабля 25 уз составляет всего 0,6 ч.
Для средних скоростей корабля порядка 15 уз время учета течения не должно превышать 0,9 … 1 ч. Большая продолжительность учета данного течения приведет к понижению точности плавания.
Приведенные здесь числовые оценочные характеристики точности счисления даже для океанского плавания являются сугубо ориентировочными, так как в отдельных регионах океана могут наблюдаться существенные отклонения вида и параметров автокорреляционных функций от среднестатистических, используемых в данном труде.
Другой вид и другие параметры автокорреляционных функций, соответствующих течениям конкретных ограниченных районов, обусловят и другие выходные данные о точности счисления.
Практическое использование способа целесообразно только при наличии персональной ЭВМ, спрограммированной по приведенным здесь формулам.
2. Средняя квадратическая погрешность счисления sc2(t), обусловленная неточностью учитываемого дрейфа.
Ветер является причиной не только ветрового (дрейфового) течения, но и дрейфа корабля. Под воздействием ветра изменяется скорость корабля и направление его перемещения. Изменение скорости учитывается лагами, а изменение направления движения учитывается введением поправки – угла дрейфа.
Найденные экспериментальным способом углы дрейфа подвержены случайным колебаниям, обусловленным случайной изменчивостью силы и направления ветра и гидродинамических ударов волн по надводной части корпуса корабля. Степень взаимосвязи случайных погрешностей учитываемого угла дрейфа для разных моментов времени характеризуется случайной функцией.
Применяя теорию случайных функций к определению дисперсии погрешностей счисления, вызванной изменчивостью углов дрейфа [15], можно получить следующую ориентировочную формулу:
 (1.6.13)
(1.6.13)
где V – скорость корабля, уз; sоa – среднее квадратическое отклонение угла дрейфа в градусах, обусловленное его изменчивостью (по данным работы [37], оно находится в пределах от 1,1 до 1,5°); Кa – коэффициент, определяемый по параметрам автокорреляционной функции дрейфа (его ориентировочное значение находится в пределах 0,3 … 0,8); t – время плавания с учетом данного угла дрейфа, ч; ![]() – средняя квадратическая погрешность способа определения угла дрейфа, градусы. При использовании современных способов определения угла дрейфа эта величина не превышает 0,5°.
– средняя квадратическая погрешность способа определения угла дрейфа, градусы. При использовании современных способов определения угла дрейфа эта величина не превышает 0,5°.
3. Средняя квадратическая погрешность счисления sc3(t), обусловленная неточностью системы курсоуказания.
При использовании современных навигационных комплексов, в состав которых входит инерциальная навигационная система, средние квадратические погрешности системы курсоуказания составляют 0,05 … 0,2°. Случайные возмущения системы демпфируются специальными устройствами, что позволяет хранить направление географического (истинного) меридиана с указанной точностью. Столь малые погрешности в курсе корабля вызывают погрешность счисления, пренебрежимо малую по сравнению с погрешностями, обусловленными неточным знанием и изменчивостью морского течения.
При счислении пути корабля по гироскопическому компасу направление истинного меридиана и, следовательно, направление истинного курса определяется с более низкой точностью.
В процессе плавания на гирокомпас воздействуют силы инерции, появляющиеся в моменты изменения скорости или курса и во время качки корабля. Эти силы вызывают затухающие инерционные погрешности, и в результате ранее определенная поправка гирокомпаса случайным образом изменяется. Этот фактор обусловливает появление нарастающей по времени случайной линейной погрешности счисления в направлении, перпендикулярном линии курса корабля.
Используя математический аппарат случайных функций способом, аналогичным способу, примененному при оценке погрешностей морских течений, можно получить дисперсию погрешностей счисления, обусловленную случайными погрешностями гирокомпаса:
![]() (1.6.14)
(1.6.14)
где ![]() – среднее квадратическое значение колебаний оси чувствительного элемента гирокомпаса (по данным [26, 32], эта величина находится в пределах от 0,4 до 0,7°); КК – коэффициент, определяемый по параметрам автокорреляционной функции, принимающий значения от 0,4 до 0,5;
– среднее квадратическое значение колебаний оси чувствительного элемента гирокомпаса (по данным [26, 32], эта величина находится в пределах от 0,4 до 0,7°); КК – коэффициент, определяемый по параметрам автокорреляционной функции, принимающий значения от 0,4 до 0,5; ![]() – средняя квадратическая погрешность поправки гирокомпаса (0,3 … 0,4°); t – время плавания по счислению, ч.
– средняя квадратическая погрешность поправки гирокомпаса (0,3 … 0,4°); t – время плавания по счислению, ч.
4. Средняя квадратическая погрешность счисления sc4(t), обусловленная ошибками измерения относительной скорости корабля.
Определенная на мерной линии поправка относительного лага имеет нестабильный характер. Для гидродинамических лагов она изменяется под влиянием дрейфа, дифферента корабля, обрастания корпуса, качки и изменения плотности морской воды. Для индукционных лагов поправка лага изменяется под влиянием нестабильности электромагнитной индукции. Параметры случайных функций изменения относительной скорости в настоящее время неизвестны [47]. Поэтому точность скорости, вырабатываемой относительным лагом, оценивается только средней квадратической погрешностью учитываемой поправки лага без учета автокорреляционной функции.
Считается, что в зависимости от способа определения поправок лага, СКП относительной скорости заключается в широких пределах: от 0,01 уз при определении поправок лага с помощью высокоточной гидрографической РНС до 0,05 уз при определении поправки лага на визуальной мерной линии.
СКП счисления, обусловленная погрешностью в относительной скорости, рассчитывается по сугубо приближенной формуле
![]() (1.6.15)
(1.6.15)
где sV – средняя квадратическая погрешность относительной скорости, уз; t – время плавания по счислению.
Подставив значения ![]() в формулу (1.6.8), можно вычислить радиальную среднюю квадратическую погрешность счисления, которая и используется для расчета вероятности навигационной безопасности плавания.
в формулу (1.6.8), можно вычислить радиальную среднюю квадратическую погрешность счисления, которая и используется для расчета вероятности навигационной безопасности плавания.
При выработке курса и пройденного расстояния современным навигационным комплексом последние два слагаемых в формуле (1.6.8) существенно меньше первых слагаемых.
При различных дисперсиях скорости течения по меридиану и по параллели слагаемые формулы (1.6.8) заменяются суммой составляющих дисперсий. В этом случае коэффициент 1,4 перед корнем заменяется на единицу.
Проблема повышения точности плавания кораблей успешно решается при использовании абсолютных лагов. При их непрерывной работе счисление ведется относительно поверхности Земли, то есть с учетом воздействия на корабль всех факторов, в том числе и морского течения. При этом исключается необходимость определения и учета основных факторов, формирующих погрешности счисления.
При использовании абсолютного лага в дискретном режиме при каждом его включении определяется вектор скорости течения [13], который учитывается в продолжении времени 0,5 … 2.0 ч.
В том случае, если на интервале счисления t (после последней обсервации) вектор скорости течения с помощью абсолютного лага определялся N раз, то радиальная СКП счисления за время плавания t от момента последней обсервации до данного момента рассчитывается по формуле (1.6.12).
Существенным препятствием практического внедрения метода оценки точности плавания по счислению на основе использования автокорреляционных функций является то, что к настоящему времени степень изученности автокорреляционных функций течения в различных регионах Мирового океана крайне низка. Изучение случайных функций течения для всего Мирового океана составляет серьезную проблему, которая вряд ли будет решена в ближайшем будущем. Можно лишь надеяться на то, что автокорреляционные функции и их параметры могут быть идентифицированы в отдельных, часто используемых кораблями, районах. Этому может способствовать наличие на современных кораблях абсолютных лагов и высокоточных среднеорбитальных КНС, с помощью которых в процессе повседневного плавания можно накопить необходимую информацию для оценки автокорреляционных функций.