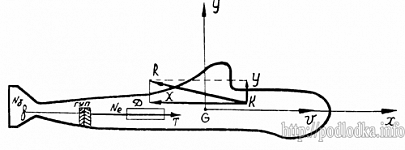
2.8. Оценка вероятности случайного выхода корабля на встречную полосу движения
Во многих случаях неогражденные смежные полосы, в которых движение совершается в противоположных направлениях, имеют одну общую границу или разделены специальной полосой, называемой полосой разделения. Если при этом полосы достаточно узкие, а в районе плавания отсутствуют средства навигационного оборудования для высокоточного определения места корабля, то не исключается возможность случайного попадания корабля на встречную полосу движения.
В п.2.1 было показано, что при плавании корабля в полосе установленного одностороннего движения на вероятность плавания, безопасного от столкновения, влияет вероятность Qвп выхода корабля из своей полосы движения в соседнюю полосу встречного движения [см. вторую формулу (2.1.8)].
Для определения вероятности такого события рассмотрим рис. 2.8.1, на котором изображены две полосы с противоположно направленным движением, разграниченные полосой разделения, ширина которой равна b. Корабль следует в расстоянии d от внутренней границы своей полосы.
Корпус корабля может оказаться в пределах соседней полосы при условии, что его случайная поперечная погрешность D будет заключаться в пределах ok < D < oa. Из рисунка следует: ok = d + b –––0,5B, oa = F + d + b + 0,5B.

При нормальном распределении случайных погрешностей местоположения корабля вероятность того, что его погрешности окажутся в указанных пределах, рассчитывается по формуле
 (2.8.1)
(2.8.1)
Здесь m – средняя квадратическая погрешность места корабля по направлению, перпендикулярному оси фарватера.
При ручных расчетах вместо этой формулы целесообразно использовать формулу, выраженную через табулированные интегралы вероятностей (функции Лапласа). При этом формула (2.8.1) преобразуется к следующему виду:
![]() (2.8.2)
(2.8.2)
При наличии сноса корабля вместо ширины корабля В используется величина В', вычисляемая по первой формуле (2.7.9).
Пример.
Корабль следует в своей полосе одностороннего движения в 2 каб от внутренней ее границы. Ширина корабля В = 0,1 каб. Ширина полосы встречного движения F = 6 каб. Ширина полосы разделения b = 2 каб. Средняя квадратическая погрешность места корабля m = 3 каб.
Определить вероятность нахождения корабля в полосе встречного движения.
Р е ш е н и е:
– с помощью таблицы приложения 1 вычисляются значения функций Лапласа – 1,0 и 0,812;
– по формуле (2.8.2) вычисляется искомая вероятность Qвп = 0,094.