4.1. Задачи и сущность статистического контроля надежности навигационных данных
Одной из причин навигационных происшествий являются промахи в решении навигационных задач или необнаруженные сбои в используемых навигационных системах. Контроль надежности решения навигационных задач и функционирования технических средств кораблевождения может производиться статистическими способами.
Современные технические средства кораблевождения, основой которых являются навигационные комплексы, рассчитаны на выработку основных навигационных данных – курса, скорости корабля и его координат – различными методами и с помощью различных навигационных систем. Измеренная избыточная навигационная информация подвергается комплексированной автоматизированной математической обработке, в результате которой определяются наиболее точные вероятнейшие навигационные данные. При этом возникает возможность контроля случайности разброса выработанных одноименных навигационных величин и выявление грубых ошибок или промахов.
Автоматизированная математическая обработка производится с помощью электронно-вычислительных машин, входящих в состав навигационного комплекса, или с помощью персональных компьютеров по заранее разработанным программам.
К сожалению,решение вероятностно-статистических задач (в том числе и задач оценки навигационной безопасности плавания) в настоящее время автоматизировано лишь частично и в минимальной степени. Тем не менее, контроль случайности различия одноименных навигационных величин и выявление промахов остается одной из важнейших задач, от правильности решения которой зависит эффективность обеспечении навигационной безопасности плавания.
Основой выявления промахов и решения перечисленных ниже задач, непосредственно связанных с точностью и надежностью кораблевождения, является выявление степени случайности различия одноименных навигационных величин, полученных от различных источников навигационной информации.
На основе контроля степени случайности разброса одноименных навигационных величин, выработанных различными средствами и методами, решаются следующие задачи, непосредственно связанные c навигационной безопасностью плавания:
– выявление промахов в результатах измерения навигационных величин, в линиях положения и в оценке места корабля;
– возможность объединения информации при ее обработке с целью повышения точности оценки той или иной величины;
– выявление систематических погрешностей навигационных систем;
– оценка различия точности выработки одноименных навигационных данных, выработанных разными методами или различными навигационными системами.
Сущность статистического способа выявления существенности (значимости) расхождения двух навигационных величин U1 и U2, имеющих случайные погрешности, основывается наследующих принципах.
Расхождение между ними является неслучайным (существенным, значимым), если оно является следствием наличия хотя бы в одной из сравниваемых величин неучтенной систематической погрешности или промаха.
Расхождение между одноименными величинами U1 и U2 является случайным (несущественным,не значимым), если оно обусловлено влиянием на них случайных факторов (например,тем, что в той и другой величине содержатся только случайные погрешности).
Для контроля случайности расхождения величин U1 и U2 вычисляется их разность DU = U1 – U2, которая сравнивается с критическим (предельным) ее значением DUР.Критическое значение DUР определяется из таблицы закона распределения величин DU для предельных вероятностей, близких к единице, то есть для Р ³ 0,99.
Вследствие столь большой вероятности, все значения DU,имеющие случайный характер, будут меньше критической величины DUР. Вероятность появления случайной величины DU, большей DUР, ничтожно мала и составляет Q = 1 – P £ 0,01 »0, то есть все DU, большие DUР, не вписываются в случайный законраспределения этой величины, и если все же такое событие (DU > DUР)произошло, то, учитывая его практическую невозможность по случайным причинам,следует заключить, что полученная разность DU неслучайна – величины U1 и U2 различаются по неслучайным причинам. Значит,различие между ними существенное, значимое (на уровне заданной вероятности Р).
Итак, если DU £DUР, то различие между U1 и U2 следует считать случайным, статистически несущественным. Сравниваемые величины не совпали по случайным причинам. Значит, они являются оценкой одной и той же искомой величины U и поэтому для расчета ее вероятнейшего значения производится объединение (в простейшем случае – осреднение) полученных величин U1 и U2. Полученный при этом результат будет ближе к истинному значению величины U, чем каждая из двух рассматриваемых величин, взятая в отдельности.
Если DU > DUР,то различие между U1 и U2 считается неслучайным, существенным, значимым. В этом случае можно заключить, что различие обусловлено или различием условий измерения, или неучтенной систематической погрешностью в одной из систем измерения,или, наконец, наличием промаха (грубой ошибки).
Каждая из этих причин исключает возможность осреднения (в общем случае, объединения) величин U1и U2. В этом случае принимаются меры к выявлению той из двух величин, которая имеет или систематическую погрешность, или грубую ошибку (сбой).
Величина DUР, ограничивающая предел случайного распределения разности DU, называется статистическим критерием.
Таким образом, для выполнения статистического контроля необходимо знать закон распределения случайной величины DU, с помощью которого определяется критическое значение DUР,соответствующее предельной вероятности, близкой к единице.
Иногда вместо закона распределения величины DU используется закон распределения ее нормированного значения К = DU/mDU,где mDU – средняя квадратическая погрешность разности DU. В этом случае сравниваются не сами разности, а их нормированные значения: если К £ КP, выбранного из таблицы нормированного распределения, то различие рассматриваемых величин U1 и U2 является случайным, если К > КP, то различие существенное, неслучайное.
В практике обеспечения навигационной безопасности плавания для расчета критических значений нормированной разности чаще всего используются нормированные величины,подчиняющиеся законам распределения Стьюдента, нормальному и закону распределения размаха.
При решении отдельных задач статистического контроля используются не разность измеренных величин, а отношение их дисперсий. В этом случае для определения критического отношения используется закон распределения Фишера-Снедокора.
4.2. Контроль и выявление промахов при решении задач обеспечения навигационной безопасности плавания
Промахи, или грубые ошибки, чаще всего являются основной причиной навигационных аварийных случаев.
Промах, или грубая ошибка – это ошибка, обусловленная резким нарушением правил измерения навигационных величин или несоблюдением правил их обработки.
Под правилами измерения понимается соблюдение установленного регламента (инструкции) при выполнении измерений с помощью той или иной навигационной системы.
Под обработкой навигационных величин понимается исправление их поправками, вычисление вероятнейших значений, использование измеренных значений для вычисления других навигационных параметров, являющихся функциями от измеренных величин, прокладка навигационных величин на навигационной карте или планшете, соотнесение измеренных величин к объекту измерения.
Нарушение правил выполнения этих функций является источником промахов.
Можно выделить четыре главных причины появления промахов:
– низкий профессиональный уровень должностных лиц штурманской службы, оценивающих навигационную обстановку, решающих навигационные задачи и контролирующих правильность результатов их решения;
– усталость вахтенного штурмана и, как следствие, его невнимательность при измерениях и при выполнении графических и вычислительных операций;
– незнание или нарушение уставных положений и правил кораблевождения, предусмотренных руководящими документами, наставлениями и инструкциями;
– неоправданно высокая самоуверенность судоводителя, его некритичность при оценке собственных действий, психологический настрой на шаблонные привычные действия, на выполнение необоснованного и неадекватного решения по управлению элементами движения корабля.
Промахи могут быть допущены на любом этапе решения задачи по обеспечению навигационной безопасности. Поэтому каждый этап должен быть проконтролирован на отсутствие промахов.
С вероятностной точки зрения промах – это погрешность той или иной навигационной величины,превышающая ее предельное значение, свойственное тому закону распределения,которому подчиняется эта величина.
Поэтому наряду с обычными методами контроля измерений и обработки (дублирование измерений и вычислений, сравнение результатов со счислимыми значениями, измерения ограждающих навигационных параметров и т. п.) для выявления промахов можно использовать статистический метод контроля.
Выявление грубых ошибок при измерении навигационных величин.
Приближенный контроль отсутствия промахов может быть произведен на основании использования нормального закона распределения по правилу «трех сигм» (трех средних квадратических погрешностей).
Известно, что предельная случайная погрешность, подчиненная нормальному закону, с вероятностью 0,997 не выходит за пределы трех СКП. Следовательно, эта величина и принимается за критическое значение.
Принимая приближенно отклонения результатов измерения от их среднего арифметического Uсрза случайную погрешность, можно заключить, что если úUэкс – Uсрú> 3m, то экстремальный результат измерения Uэкс с вероятностью 0,997содержит грубую ошибку. Он исключается из данной серии измерения и не участвует в дальнейшей обработке.
Степень приближенности этого способа уменьшается по мере увеличения количества измерений n данной навигационной величины. При n > 30 способ может использоваться, как основной. Но, к сожалению, в навигационной практике количество измерений одной и той же величины, как правило, ограничено и находится в пределах трех–семи.
В этих типичных для навигации случаях используется способ выявления промахов, основанный на законе распределении размаха [8].
При этом может быть два варианта выявления промаха: при неизвестной средней квадратической погрешности результата единичного измерения и при известной СКП.
В первом случае все результаты измерения приводятся к одному моменту времени и из них выбираются три результата: два экстремальных Uэкс (максимальный Umax и минимальный Umin) и ближайший к подозрительному из экстремальных – U'. После этого рассчитывается размах R = Umax – Umin и вычисляется разность r = =úUэкс – U'ú.
Если r £ QR, то проверяемый экстремальный результат промаха (грубой ошибки) не содержит.
Если r > QR, тов проверяемом экстремальном результате содержится грубая ошибка. Этот результат измерения исключается из дальнейшей обработки.
Численные значения величины Q зависят от количества измерений n и от заданной вероятности оправдываемости вывода. Они приведены в табл. 4.2.1.
Т а б л и ц а4.2.1
| Р | Количество измерений n | |||||||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | 20 | |
| 0,990 0,995 | 0,988 0,994 | 0,889 0,926 | 0,780 0,821 | 0,698 0,740 | 0,637 0,680 | 0,590 0,634 | 0,555 0,598 | 0,527 0,568 | 0,438 0,475 | 0,391 0,425 |
Пример.
После измерениярадиолокатором расстояний до неподвижной цели и приведения их к одному моментуполучены следующие результаты (мили): 12,3; 11,8; 14,9; 12,0 и 11,9.
Выявить наличиепромахов в результатах измерений с доверительной вероятностью 0,99.
Р е ш е н и е.
а) Проверяется напромах максимальный результат, для чего:
– вычисляетсяразмах R = 14,9 – 11,8 = 3,1 мили;
– рассчитывается r= 14,9 – 12,3 = 2,6 мили;
– из табл. 4.2.1 поn = 5 и по доверительной вероятности Р = 0,99 выбирается Q = 78 ирассчитывается произведение QR = 2,4 мили.
Так как r > QR (2,6 > 2,4), то третье измерение содержит грубую ошибку. Оно исключается издальнейшей обработки.
б) Проверяетсяминимальный результат:
– после исключениямаксимального значения вычисляется новый размах R' = 12,3 – 11,8 = 0,5 мили;
– рассчитывается r'= ú 11,8 – 11,9ú = 0,1 мили;
– по n = 4 и по Р= 0,99 из табл. 4.2.1 величина Q = 0,89;
– вычисляетсяпроизведение QR' = 0,44 мили и сравнивается с r'.
Так как r' <QR', то в минимальном результате промаха нет.
Рассмотрим другойвариант, когда известна СКП измерений (определена по результатам ранеевыполненных измерений в аналогичных условиях).
В этом случаерассчитывается нормированный размах W = R/m, который сравнивается с табличнымкритическим значением WР.
Критическиезначения WР нормированного размаха для доверительных вероятностей 0,99 и 0,995представлены в табл. 4.2.2.
Если W £ WР, то полученный размах укладываетсяв норму случайного закона распределения – грубой ошибки в измерениях нет.
Если W >WР, торазброс измерений чрезмерно большой, он не соответствует норме случайногоразброса, следовательно, в одном из экстремальных результатов содержится грубаяошибка.
Т а б л и ц а4.2.2
| Р | Количество измерений n | |||||||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | 20 | |
| 0,990 0,995 | 4,12 4,42 | 4,40 4,69 | 4,60 4,89 | 4,76 5,03 | 4,88 5,15 | 4,99 5,26 | 5,08 5,34 | 5,16 5,42 | 5,45 5,70 | 5,65 5,89 |
Пример.
Условияпредыдущего примера. СКП единичного измерения расстояния m= = 0,6 мили. Выявитьналичие промахов.
Р е ш е н и е:
– вычисляетсянормированный размах W = R / m = 5,17;
– из табл. 4.2.2по n = 5 и P = 0,99 выбирают критическое значение размаха WР = 4,60.
Так как W > WР,то следует вывод о том, что в одном из экстремальных результатов измерениясодержится промах.
Выявление грубыхошибок в линиях положения.
Оценка навигационнойобстановки и расчет навигационной безопасности плавания производится на основепоказателей, характеризующих точность места корабля. Обсервованное место определяетсяпо линиям положения, соответствующим измеренным навигационным параметрам. Еслихотя бы в одной из линий положения содержится промах, то обсервованное местоокажется неверным.
При ненадежномсчислимом месте для выявления промахов в линиях положения статистическимспособом их количество должно быть не менее пяти (n ³ 5).
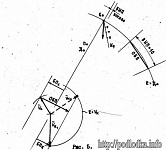
По всем (в общемслучае неравноточным) обсервованным линиям положения находится вероятнейшееместо корабля – точка В (рис. 4.2.1).
Измеряютсяотклонения vi каждой i–й линии положения от вероятнейшего места. Случайностьотклонения обусловлена случайной погрешностью точки В (оценивается радиальнойСКП MB) и случайной погрешностью линии положения (оценивается СКП mлп i = mUi /g).
Поэтому предельное (критическое) случайное отклонение линии положения от вероятнейшего местахарактеризуется величиной
где zР –коэффициент, определяемый из таблицы приложения 1 по заданной доверительнойвероятности, не меньшей 0,99.

Если отклонение
Если имеетсяобоснованная уверенность в том, что счислимое место не содержит грубой илисистематической ошибки, то промахи в линиях положения можно выявлять по ихотклонениям от счислимого места. При этом в формулу критического отклонения (4.2.1) вместо MB подставляется радиальная СКП счислимого места. Прииспользовании этого способа количество линий положения может быть любое – от 1до n.
Пример.
Определили местопо пяти неравноточным линиям положения и рассчитали его радиальную СКП МВ =1,4 мили. Длины отклонений – перпендикуляров v, опущенных из вероятнейшегоместа на линии положения, приведены в таблице:
| Номер линии положения | 1 | 2 | 3 | 4 | 5 |
| v, мили | 3,2 | 4,9 | 2,8 | 4,4 | 5,0 |
| mлп, мили | 1,2 | 2,0 | 1,0 | 1,0 | 1,6 |
Выявить наличиепромахов в линиях положения с доверительной вероятностью 0,997.
Р е ш е н и е:
– по доверительнойвероятности 0,997 из таблицы приложения 1 находится коэффициент zP = 3,0;
– по формуле (4.2.1) вычисляются критические значения для каждой линии положения: 4,65;6,69; 4,20; 4,20; 5,64.
Сравнениеотклонений с соответствующими критическими значениями приводит к заключению,что в четвертой линии положения отклонение (4,4) больше критического (4,20). Следовательно,четвертая линия положения содержит грубую ошибку.
Если приненадежном счислимом месте обсервация производилась по трем линиям положения,образовавшим треугольник погрешностей, который по условиям плавания нельзяпринять за малый, то для выявления промахов в линиях положения используетсялогика отличия систематических погрешностей от грубых ошибок: систематическаяпогрешность содержится во всех линиях положения, а грубая ошибка чаще всего водной из них. Опираясь на это положение, промахи выявляются следующим образом.
При образованиибольшого треугольника погрешностей необходимо произвести повторные измерениянавигационных параметров относительно тех же ориентиров. При этом могут быть следующиеварианты.
а) Треугольникпогрешностей уменьшился до пренебрежимо малых размеров. Делается вывод о том,что в предыдущей серии измерений в одной из линий положения (по крайней мере)содержалась грубая ошибка. Вероятнейшее место определяется по результатамвторой серии измерений.
б) Конфигурация иразмеры нового треугольника погрешностей существенно не изменились, то естьразличие соответствующих навигационных параметров после их приведения к одномумоменту не выходит за пределы их случайной вариации.
Количественнымкритерием несущественного изменения фигуры погрешностей является соблюдение длявсех измеренных навигационных параметров условия
÷ Ui'' – (Ui' + DUi)÷£ 3 mUi, (4.2.3)
где Ui' и Ui'' –результаты измерения
Соблюдение этогоусловия является свидетельством того, что навигационные параметры содержатсистематическую или повторяющуюся погрешность. Утверждать о наличии промаховоснований нет.
в) Конфигурация иразмеры нового треугольника погрешностей изменились существенно и при этомусловие (4.2.3) не соблюдается для всех параметров. Учитывая, что промахи вовсех линиях положения маловероятны, делается заключение о несоответствиипринятых в расчет СКП навигационных параметров их фактическим значениям.
Если присущественном изменении фигуры погрешностей условие (4.2.3) не соблюдается лишьдля одного навигационного параметра, то линия положения, соответствующая этомупараметру, содержит промах.
В общем же случаепри появлении большой фигуры погрешностей целесообразно перейти к определениюместа с помощью другой навигационной системы.
Выявление грубыхошибок в обсервованных местах.
При правильномвыборе способа нахождения вероятнейшего места (по составу погрешностейобсервованных навигационных параметров) промах в обсервованном месте обнаруживаетсяпри наличии нескольких обсерваций, полученных по одной и той же навигационнойсистеме (приведенных к одному моменту).
Сущностьприближенного способа выявления промахов в обсервациях состоит в следующем.

На карте снанесенными обсервациями (рис. 4.2.2) измеряются размахи широты Rj и долготы Rlкак разности их экстремальных значений. Измеряются также разности между двумякрайними одноименными координатами, одна из которых является подозрительнойэкстремальной, – величины rj и rl.
По табл. 4.2.1 определяетсякоэффициент Q и рассчитываются произведения QRjи QRl. Далее производятся сравнения rj с QRjи rl с QRl.
Если хотя бы одноиз значений r окажется больше соответствующего произведения, то вподозрительной экстремальной координате содержится грубая ошибка. Обсервация спромахом в любой из координат считается недостоверной.
При наличии толькодвух обсерваций, приведенных к одному моменту, их контроль производится посравнению расстояния между ними d с критическим, соответствующим суммарнойпредельной погрешности мест по направлению линии между обсервациями.
В одной изобсерваций содержится грубая ошибка, если соблюдается неравенство
 (4.2.4)
(4.2.4)
где ![]() и
и ![]() –
–
При обсервациях сиспользованием радионавигационных систем промахи могут быть следствиемневерного разрешения многозначности.
Для правильногоразрешения многозначности импульсно-фазовых РНС необходимо, чтобы погрешность импульсныхизмерений была меньше половины периода несущих колебаний.
Для правильногоразрешения многозначности фазовых РНС необходимо, чтобы предельная радиальнаяСКП счислимого места была меньше половины ширины грубо-разностной фазовой дорожки.Были случаи, когда пренебрежение таким контролем приводило к серьезнымнавигационным происшествиям (например, посадка на мель советской подводнойлодки в районе шведской
При контролеобсерваций, полученных в открытом море с использованием избыточныхнавигационных параметров (по высотам светил, по радиопеленгам, поимпульсно-фазовым РНС на пространственной радиоволне, по РНС"Омега"), следует учитывать следующее обстоятельство.
Линии положенияпри обсервациях этими способами, как правило, образуют фигуру погрешностей,поэтому вероятнейшее место отыскивается обобщенным методом наименьших квадратов.Но при малой избыточности навигационных параметров, свойственной практикеопределениям места, точность и надежность этого метода не всегда соответствуюттребованиям современного судовождения. Это проявляется в том, что фигурапогрешностей, в которой согласно методу наименьших квадратов расположено вероятнейшееместо, на самом деле не всегда является той площадью, в которой находитсяфактическое (действительное) место корабля.
Исследования [21]показали, что вероятность накрытия истинного места фигурой погрешностей приобсервации по трем взаимонезависимым навигационным параметрам составляет всего25%. С ростом коэффициента корреляции от нуля до единицы эта вероятность падаетдо нуля при расположении градиентов в одной половине горизонта и увеличиваетсяпрактически до 100% при расположении градиентов по всему горизонту.
Несколькооптимистичнее выглядит ситуация при определении места по четырем линиямположения. При взаимонезависимых навигационных параметрах вероятность накрытияистинного места увеличивается в два раза и составляет 50%. При зависимых параметрахобщая закономерность изменения вероятности накрытия остается такой же, как ипри независимых навигационных параметрах, но количественно она выражаетсяпо-другому.
Проблемаадекватности обсервации действительному месту корабля и, следовательно,проблема надежности места при малом количестве навигационных параметров сопределенной степенью надежности решается тремя способами:
– использованиемобобщенного метода квадратов и его приближенных графоаналитических аналогов,учитывающих количественное соотношение частных и повторяющихся погрешностей[12] и приводящих к получению вероятнейшего места (при наличии корреляции запределами) фигуры погрешностей;
– увеличениемколичества измеряемых навигационных параметров. Чем больше избыточностьнавигационной информации, тем ближе вероятнейшее место к действительному;
– повышениемточности навигационных параметров. При высокоточных навигационных параметрахплощадь фигуры погрешностей уменьшается до пренебрежимо малых размеров и приэтом вероятнейшее место практически совпадает с действительным местом корабля.
Выявление промаховв счислимом месте.
Счисление путиявляется основой решения всех задач кораблевождения, в том числе и его главнойзадачи – обеспечения навигационной безопасности плавания. Поэтому контрольсчисления и счислимых мест на предмет отсутствия в них промахов является однимиз важнейших условий предотвращения навигационных происшествий, связанных спосадкой корабля на мель или с касанием грунта.
Промах в счислимомместе может быть обнаружен после обсервации путем анализа невязки. Невязкиявляются обобщенной информацией, характеризующей точность ведения навигационнойпрокладки. Причины невязок – погрешности счисления и погрешности обсерваций.При надежных высокоточных обсервациях невязки являются следствием погрешностейсчисления. В этом случае анализ счисления на промах производится следующим образом.
После каждойобсервации вычисляются два критических значения невязки – ее предельноеслучайное значение ![]() ,обусловленное только случайными погрешностями последней и данной обсерваций, ипредельное значение случайной невязки
,обусловленное только случайными погрешностями последней и данной обсерваций, ипредельное значение случайной невязки ![]() , обусловленное погрешностями обсерваций исчисления:
, обусловленное погрешностями обсерваций исчисления:
 (4.2.5)
(4.2.5)
где kP –коэффициент кругового закона распределения Релея, определяемый по доверительнойвероятности, не меньшей 0,99, с помощью таблицы приложения 4, а также табл. 1-вМТ-75 или табл. 4.14 НМТ; ![]() – радиальные СКП предыдущей и данной обсерваций;
– радиальные СКП предыдущей и данной обсерваций;![]() – радиальная СКПсчисления на интервале между двумя последними обсервациями.
– радиальная СКПсчисления на интервале между двумя последними обсервациями.
Для контролясчисления производится сравнение полученной невязки Сi с ее критическимивеличинами. При этом может реализоваться один из следующих трех вариантов.
Если Сi <, то с заданнойвероятностью можно считать, что невязка является следствием неточности предыдущейи данной обсерваций. Промаха в счислении нет. В счислимом месте могут бытьпогрешности, которые, однако, не проявляются на фоне погрешностей обсерваций.
Если соблюдаетсяусловие ![]() < Сi £
< Сi £ ![]() , то делается вывод о том, что промахов всчислении и счислимом месте нет. Но поскольку невязка превышает предельнуюпогрешность обсерваций, то принимаются меры по уточнению элементов счисления ив первую очередь по уточнению элементов сноса корабля течением и ветром.
, то делается вывод о том, что промахов всчислении и счислимом месте нет. Но поскольку невязка превышает предельнуюпогрешность обсерваций, то принимаются меры по уточнению элементов счисления ив первую очередь по уточнению элементов сноса корабля течением и ветром.
Если Сi >, то в счислимом местесодержится грубая ошибка или неучтенная систематическая погрешность. В этом случаепроверяется правильность навигационной прокладки от предыдущей обсервации доданной, и если ошибок (промахов) не обнаружено, то делается вывод осущественном изменении элементов сноса. Принимаются меры к их уточнению.
4.3. Контроль надежности работы навигационных систем
В некоторыхслучаях причиной навигационного происшествия может стать незамеченный сбой (разрегулировка) навигационной системы, вырабатывающей навигационные величины.
Если на кораблеимеется несколько систем, вырабатывающих параметры одного наименования, токонтроль надежности их работы производится с помощью статистического критерияна основе сравнения одноименных параметров
Рассмотрим дваварианта контроля.
1. Сравниваемыенавигационные системы обладают одинаковой точностью, то есть вырабатываемые иминавигационные величины являются равноточными. Их СКП одинаковы и равны m.
В этом случаеодновременно по каждой из этих систем определяются вероятнейшие навигационныевеличины U1 и U2 и рассчитываются нормированные разности:
t = ú U1 – U2ú / mDU, (4.3.1)
где mDU – суммарная средняя квадратическаяпогрешность сравниваемых навигационных систем.
Если дляопределения вероятнейшего значения по каждой системе было произведено по n измерений,то
![]() (4.3.2)
(4.3.2)
В курсематематической статистики показано, что нормированная случайная разностьвероятнейших значений t подчиняется закону распределения Стьюдента или t-распределению.
Поэтому, опираясьна общий принцип статистического контроля, изложенный в п.4.1, можно проверитьслучайность расхождения показаний двух систем.
Если t £ tP, то различие навигационных величинU1 и U2 несущественно и обусловлено случайными причинами. Обе навигационныесистемы работают стабильно, без сбоя. Оба показания объединяются, и в расчетпринимается их среднее арифметическое значение.
Критическоезначение tP, соответствующее заданной доверительной вероятности Р, определяетсяпо таблице распределения Стьюдента, приведенной в приложении 6, по аргументу (2n– 2).
Если t > tP,то различие между показаниями рассматриваемых систем существенное, неслучайное (на уровне вероятности Р). Это значит, что в одной из систем произошелсистематический сдвиг (возможно, сбой) или за счет ее разрегулирования, или
2. При использованиинеравноточных систем, вырабатывающих одноименные навигационные величины со среднимиквадратическими погрешностями m1 и m2, критерием случайного различия ихпоказаний является условие
 (4.3.3)
(4.3.3)
Критическоезначение нормированной разности tP определяется по таблице распределенияСтьюдента (по аргументам Р и в данном случае по n).
При выполненииусловия (4.3.3) делается заключение о том, что обе навигационные системы врабочем состоянии и при расчете навигационной безопасности используется среднеевзвешенное значение параметра U.
Если условие (4.3.3) не выполняется, то показания одной из систем содержат или неучтеннуюсистематическую погрешность, или грубую ошибку. Принимаются меры к выявлениюэтой системы.
Пример.
По двумкурсоуказателям, средние квадратические погрешности которых m1 = 0,5o и m2 =0,2o, в результате одновременных пятикратных измерений и исправления их своимипоправками определены вероятнейшие значения курса судна: К1 = 243о и К2 = 246о.
Выявить надежностьработы курсоуказателей с доверительной вероятностью 0,99.
Р е ш е н и е:
– рассчитываетсяразность вероятнейших курсов DК = 3,0о;
– из табл.приложения 6 по Р = 0,99 и n = 5 определяется критическое значениенормированной разности tP = 4,60;
– вычисляетсясуммарное значение СКП – величина mDU =0,24о;
– проверяетсясоблюдение условия (4.3.3): так как левая часть этого неравенства (3,0о) большеправой части (1,1о), то делается заключение о том, что, по крайней мере, водном из курсоуказателей содержится или неучтенная систематическая погрешность,или произошла его разрегулировка.
4.4. Вероятность появления экстремальных погрешностей
Исходными даннымидля анализа степени навигационной безопасности плавания являются точностныехарактеристики навигационных величин – навигационных параметров и координат корабля.При оценке погрешностей этих величин, как правило, исходят из нормальногозакона их распределения. С позиций центральной предельной теоремы теориивероятностей такой подход является вполне обоснованным.
Согласнонормальному закону все погрешности с вероятностью 0,997 укладываются в пределытрех СКП.
В работе [23]изложен закон распределения наибольших или экстремальных величин. Используемего для оценки вероятности наибольших (экстремальных) случайных погрешностей.
Наибольшимипогрешностями в сериях случайных погрешностей считаются такие, абсолютныезначения которых ú±Dm÷ = z превышают модули всех другихпогрешностей данной серии.
Исследованиемустановлено, что совокупность максимальных погрешностей, выбранных из различныхнезависимых серий измерений, подчиняется двойному экспоненциальному закону,функция распределения которого выражается формулой
![]() (4.4.1)
(4.4.1)
где z – заданноезначение наибольшей погрешности; a и q– параметры распределения: a –нормированное среднее квадратическое отклонение показателя экспоненты; q – модаданного распределения – значение погрешности, обладающей наибольшей плотностьюраспределения.
Вероятностьпоявления погрешности, превышающей заданную наибольшую, вычисляется по формуле
P = 1 – F (z). (4.4.2)
Плотностьраспределения случайных погрешностей, подчиненных двойному экспоненциальномузакону распределения, выражается формулой
![]() (4.4.3)
(4.4.3)
Кривая плотностираспределения изображена на рис. 4.4.1.

Заштрихованная нарисунке площадь соответствует вероятности появления погрешности, превышающейзаданную величину z.
Для оценкипараметров a и q введем обозначение
y = a (z – q). (4.4.4)
Математическоеожидание этой величины равно
М (y) = aМ (z) – aq.
Отсюда
q = М (z) – М (y) / a.
Приняв за М (z)среднее арифметическое значение модулей наибольших погрешностей, вычисленное понаибольшим выборкам из нескольких серий измерений, – величину ![]() и обозначив для краткости М (y) =, будем иметь
и обозначив для краткости М (y) =, будем иметь
 (4.4.5)
(4.4.5)
Для оценкивеличины a определим среднееквадратическое отклонение функции (4.4.4): sу= asz,где sz – среднее квадратическоеотклонение наибольшей погрешности z. Отсюда
![]() (4.4.6)
(4.4.6)
Значения и sу приведены в табл. 4.4.1, входным аргументомкоторой является величина N – количество серий нормально распределенныхнезависимых случайных погрешностей, в каждой из которых определяется однанаибольшая погрешность.
Т а б л и ц а4.4.1
| N |
| sу | N |
| sу | N |
| sу |
| 8 10 12 14 | 0,484 0,495 0,504 0,510 | 0,904 0,950 0,983 1,009 | 16 18 20 25 | 0,516 0,520 0,524 0.531 | 1,032 1,049 1,063 1,092 | 30 35 40 50 | 0,536 0,540 0,544 0,548 | 1,112 1,129 1,141 1,161 |
Таким образом,чтобы воспользоваться формулой (4.4.1) для расчета вероятности невыходапогрешности за пределы заданного наибольшего значения, необходимо иметьстатистическую информацию о погрешностях, полученных в N независимых сериях обычныхизмерений. В каждой серии, состоящей из 25 и более измерений, определяетсянаибольшая по модулю погрешность и по их совокупности вычисляется среднееарифметическое значение наибольшей погрешности и ее среднее квадратическоеотклонение:
 (4.4.7)
(4.4.7)
Периодповторяемости максимальной погрешности, превышающей заданную, рассчитывается поформуле
 (4.4.8)
(4.4.8)
Вычислив величину Т,можно заключить, что в среднем в каждой
Расчеты показывают,что повторяемость экстремальных погрешностей, вычисленная по двойному экспоненциальномузакону, существенно выше повторяемости той же погрешности, найденной понормальному закону распределения.
Пример.
В одинаковыхусловиях было получено 16 серий погрешностей радионавигационного параметра и изкаждой серии выбрана наибольшая по модулю погрешность. С помощью формул (4.4.7)вычислены средняя арифметическая наибольшая погрешность и ее среднееквадратическое отклонение: ![]() sz =0,6 мкс.
sz =0,6 мкс.
Определитьвероятность того, что погрешность радионавигационного параметра превыситвеличину z = 5 мкс и частоту появления погрешности, превышающей это значение.
Р е ш е н и е:
– из табл. 4.4.1по N = 16 выбираются значения ![]() = 0,516 и sу=1,032 и по ним с помощью формул (4.4.6) и (4.4.5) вычисляются параметры a = 1,72 и q = 3,7;
= 0,516 и sу=1,032 и по ним с помощью формул (4.4.6) и (4.4.5) вычисляются параметры a = 1,72 и q = 3,7;
– по формуле (4.4.2) с использованием выражения (4.4.1) вычисляется вероятность того, чтонаибольшая погрешность превысит 5 мкс: Р = 0,101;
– по формуле (4.4.8) рассчитывается период повторяемости погрешности, превышающей 5 мкс: Т =9,9 » 10. Это значит, что погрешности,превышающие 5 мкс, будут появляться в среднем один раз в каждой десятой серииизмерений.
Вероятностьпоявления максимальных погрешностей целесообразно учитывать в предварительныхрасчетах навигационной безопасности плавания в условиях, когда требуется вмаксимальной степени уменьшить риск навигационного происшествия.
В процессеплавания учет наибольших погрешностей при оценке навигационной безопасностиплавания может производиться с помощью автоматизированного статистическогомоделирования серий случайных нормально распределенных погрешностей для каждойсредней квадратической погрешности места судна по направлению на опасность. Поэтим данным ЭВМ по заранее введенной в нее программе вычисляет параметрыдвойного экспоненциального закона распределения и оценивает вероятность ипериод появления заданной наибольшей погрешности. За заданную наибольшую погрешностьв этом случае принимается погрешность, равная расстоянию до ближайшейнавигационной опасности.
Вероятностьпоявления наибольших погрешностей или погрешностей, превышающих заданнуюнаибольшую погрешность, важно учитывать при проектировании ширины фарватеров иполос установленного движения. Расчет при этом должен быть ориентирован наточность тех средств навигационного оборудования, которыми будет оборудованрайон плавания с проложенным фарватером.
Особо актуаленвопрос учета наибольших погрешностей при оборудовании фарватеров в районахминной опасности.