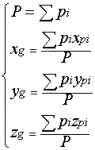2. Основы построения АП АП
а) Принцип определения счислимых координат.
Из теории навигации известно, что счислимые координаты места корабля при аналитическом счислении определяются зависимостями:
(1)где: j0 и l0 – начальные широта и долгота;
РШ и РД – соответственно разность широт и разность долгот.
РШ определяется приращением: jС — j0.
РД определяется выражением
РД = ОТШ × sec jCР (2)
где: ОТШ – отшествие,
jСР – средняя широта между начальной (j0) и текущей (jС) широтой места.
Т.о. чтобы иметь счислимые координаты необходимо знать начальные координаты (а они известны и вводятся вручную в начале автоматического счисления) и непрерывно вычислять РШ и РД (решение этой задачи происходит в СРУ).
Рассмотрим принцип выработки РШ и РД, для чего обратимся к рис. 1.
На рис. 1 дополнительно обозначено:
ПУ = КК + DК + a + b — путевой угол;
V – скорость корабля по лагу с учетом вводимых поправок;
t – время движения.
Из рисунка 1 очевидны следующие соотношения:
(3)
В период плавания корабля непрерывно меняются значения РШ и РД. В СРУ непрерывно вычисляются бесконечно малые промежутки времени (dt) и происходит непрерывное их суммирование.
Процедура суммирования бесконечно малых величин определяется таким математическим действием как интегрирование.
Представив РШ и РД в виде суммы элементарных приращений, получим:
(4)
По выражениям (4) в СРУ непрерывно вырабатываются текущие значения РШ и РД, которые прибавляются к начальным координатам (j0; l0).
Подставляя выражения (4) в (1) получим выражение (5) по которым в СРУ решается задача автоматического вычисления счислимых координат:
(5)
Алгоритм выработки счислимых координат представлен на рис. 2.
Структурная схема алгоритма выработки счислимых координат
Таким образом, в автопрокладчике решается задача вычисления счислимых координат.
Рассмотрим принцип ведения автоматической графической прокладки пути корабля.
б) Принцип ведения автоматической прокладки
Автоматическая графическая прокладка пути корабля ведется на МНК с помощью специального электромеханического планшета и заключается в построении вектора пройденного расстояния (S) по составляющим РШ и ОТШ, которые вырабатываются СРУ.
Векторное сложение двух этих величин можно пояснить простейшим рисунком:
Рис. 3.
Из рис. 3:
, (6)
где S – вектор пути корабля;
РШ и ОТШ – составляющие пройденного расстояния по меридиану и параллели соответственно.
В качестве МНК в кораблевождении используются карты в нормальной проекции Меркатора.
Одной из характерных особенностей этой проекции является то, что масштаб переменный в различных точках карты (т. е. текущий масштаб). Поэтому для ведения автоматической прокладки на картах в меркаторской проекции необходимо иметь составляющие пройденного расстояния по меридиану (РШ) и параллели (ОТШ) в текущем масштабе карты.
Текущий масштаб карты является функцией экваториального масштаба и широты плавания корабля:
МТ = МЭsecjC, (7)
где МТ – текущий масштаб карты;
МЭ – экваториальный масштаб карты (величина постоянная для данной карты).
Составляющие пройденного расстояния по меридиану и параллели в текущем масштабе карты определяются выражением:
(8)
Подставляя в (8) значения РШ и ОТШ (из выражения 4) и принимая 
, где СЭ – знаменатель экваториального масштаба, получим:
(9)
Значения 
поступают на специальное устройство, где происходит их механическое сложение, и суммарный вектор 
с помощью отмечающего устройства прокладывается на карте.
Таким образом, в АП решается задача автоматической прокладки пути корабля.
Добавить комментарий