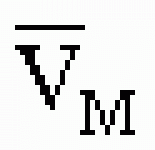Динамической остойчивостью называется способность подводной лодки выдерживать, не опрокидываясь, динамическое воздействие сил и моментов, вызывающих её наклонение.
В отличие от статического динамическое воздействие сил и моментов (шквального ветра, взрывной волны) сообщает подводной лодке значительные угловые скорости и ускорения.
Анализ поведения подводной лодки при воздействии на нее динамического кренящего момента можно провести на диаграмме статической остойчивости. При этом используется теорема кинетической энергии, согласно которой приращение кинетической энергии наклонения подводной лодки равно работе действующих на неё сил.
Рис. 24. Воздействие на подводную лодку кренящего динамического момента.
Как показано на рис. 24, к подводной лодке, плавающей без крена, внезапно прикладывается кренящий момент mкр дин, величина которого остается постоянной при изменении крена подводной лодки. Подводная лодка получает положительное ускорение, с которым начинается её наклонение на правый борт. По мере наклонения возрастает восстанавливающий момент, но вначале он будет меньше кренящего до угла крена θcт, при котором mкр = mθ. Благодаря этому наклонение подводной лодки будет совершаться ускоренно. Когда подводная лодка достигает статического положения равновесия, определяемого из условия mкр = mθ, кинетическая энергия ее вращательного движения будет максимальной. Поэтому подводная лодка не останется в положении равновесия, а за счет кинетической энергии будет наклоняться дальше, но замедленно, поскольку восстанавливающий момент больше кренящего. Накопленная ранее кинетическая энергия погашается избыточной работой восстанавливающего момента. Как только величина этой работы будет достаточной для полного погашения кинетической энергии, угловая скорость станет равной нулю и подводная лодка перестанет крениться.
Наибольший угол наклонения, которого достигает подводная лодка при воздействии на неё динамического момента, называется динамическим углом крена θдин. В отличие от него угол крена, с которым подводная лодка будет плавать под действием того же момента и который определяется из условия mкр = mθ, называется статическим углом крена θст.
Достигнув динамического угла крена θдин, подводная лодка не будет в равновесии и под действием избыточного восстанавливающего момента начнёт ускоренно спрямляться. При отсутствии сопротивления воды подводная лодка стала бы совершать незатухающие колебания около положения равновесия при крене θст с амплитудой от 0 до θдин. Но практически под влиянием сопротивления воды колебания подводной лодки быстро затухают и она остается плавать со статическим углом крена θст.
Динамическое воздействие кренящего момента всегда опаснее статического, так как приводит к более значительным наклонениям подводной лодки. Для оценки безопасности подводной лодки при действии различных кренящих моментов важнейшее значение имеет определение динамического угла крена.
Динамический угол крена может быть определен из условия равенства по абсолютной величине работ кренящего Ткр и восстанавливающего Тθ моментов при наклонении подводной лодки от исходного прямого положения до динамического угла крена: Ткр = Тθ.
Поскольку работа момента определяется как произведение момента на угол поворота, то элементарная работа кренящего момента будет dТкр = mкрdθ, а элементарная работа восстанавливающего момента dТθ = mθdθ. Тогда работа кренящего момента при наклонении подводной лодки от прямого положения до динамического угла крена определяется выражением 
, а работа восстанавливающего момента при этом же наклонении 
Геометрически на диаграмме статической остойчивости работа восстанавливающего момента представляет собой площадь под графиком восстанавливающего момента OBCDE, а работа кренящего момента — площадь под графиком кренящего момента OABDE (рис. 25). При достижении подводной лодкой динамического угла крена Ткр = Тθ, т. е. площадь OBCDE равна площади OABDE, а поскольку эти площади имеют общую часть OBDE, то для определения динамического угла крена необходимо и достаточно, чтобы площадь ОАВ (избыток работы кренящего момента до угла θст) была равна площади BCD (избыток работы восстанавливающего момента за точкой статического равновесия).
Таким образом, для определения динамического угла крена по диаграмме статической остойчивости необходимо:
— нанести на диаграмму график кренящего момента, при этом абсцисса точки пересечения В двух графиков даст θст, а площадь ОАВ показывает избыток работы кренящего момента;
— провести ординату ЕС таким образом, чтобы площадь BCD была равна площади ОАВ, абсцисса этой ординаты даст динамический угол крена θдин.
В пределах прямолинейной части диаграммы статической остойчивости, как видно на рис. 25, динамический угол крена в два раза больше статического: θдин ≈ 2θст.
Поскольку величина динамического угла крена зависит от работы восстанавливающего момента, то эта работа служит мерой динамической остойчивости подводной лодки. Максимальное значение работы восстанавливающего момента имеет место при накренении подводной лодки из прямого положения до угла заката:
.
На диаграмме статической остойчивости эта работа выражается площадью под графиком mθ между θ=0 и θ=θз. Эта величина определяет запас динамической остойчивости подводной лодки, плавающей без крена.
При плавании подводной лодки с креном запас динамической остойчивости определяется площадью диаграммы, расположенной выше графика кренящего момента, создающего этот крен. Запас динамической остойчивости имеет важнейшее значение для обеспечения безопасности подводной лодки. Чем больше запас динамической остойчивости, тем лучше обеспечивается безопасность подводной лодки при действии на нее динамически приложенных кренящих моментов.
С помощью диаграммы статической остойчивости можно определить наибольший динамический угол крена и наибольший динамический кренящий момент, который может выдержать подводная лодка, не опрокидываясь. Эти величины находятся из условии равенства избытка работы восстанавливающего момента (площадь BCК, рис. 26) и избытка работы максимального кренящего динамического момента (площадь ОАВ). Ордината точки К определяет максимальный динамический кренящий момент, который выдерживает подводная лодка, а абсцисса точки К дает предельный угол динамического наклонения. Из рис. 26 видно, что mкр ст mах > mкр дин mах, а θст mах < θдин mах.
Рис. 26. Определение пределов динамической остойчивости
Диаграмма статической остойчивости, удобная для определения статических углов крена и предельных величин статически приложенных моментов, мало приспособлена для определения динамических углов крена и предельных динамических крепящих моментов. Эти динамические характеристики с помощью диаграммы статической остойчивости определяются путём подбора площадей.
Значительно проще эти задачи решаются с помощью диаграммы динамической остойчивости. Диаграмма динамической остойчивости—это график зависимости работы восстанавливающего момента от угла крена Tθ =f (θ), который рассчитывается и строится при проектировании подводной лодки.
Так как , то диаграмма динамической остойчивости представляет собой интегральную кривую по отношению к диаграмме статической остойчивости (рис. 27). Из свойств интегральной кривой следует:
— любая ордината диаграммы динамической остойчивости представляет собой площадь под диаграммой статической остойчивости по эту ординату (ордината ВС выражает в масштабе площадь ОАВ);
— точка перегиба диаграммы динамической остойчивости соответствует максимуму диаграммы статической остойчивости;
— максимум диаграммы динамической остойчивости соответствует углу заката диаграммы статической остойчивости.
Рис. 27. Диаграммы статической и динамической остойчивости
По диаграмме динамической остойчивости определяются:
— угол крена при динамическом воздействии кренящего момента;
— предельный динамический кренящий момент, который может выдержать подводная лодка;
— предельный угол динамического наклонения подводной лодки.
Для решения этих задач необходимо на диаграмме динамической остойчивости построить график работы кренящего момента Tкp=f (θ).
При mкр = const 
= mкрθ. Следовательно, графиком работы кренящего момента является прямая, проведенная из начала координат с угловым коэффициентом mкр. Поэтому построение графика работы кренящего момента производится следующим образом. На оси углов откладывается угол, равный одному радиану, в полученной точке А (рис. 28) восстанавливается перпендикуляр, на котором в масштабе откладывается величина кренящего момента (отрезок АВ). Луч, проведенный из начала координат через ординату на перпендикуляре, соответствующую кренящему моменту, и представляет собой график работы кренящего момента. Это построение основано на том, что угловой коэффициент tgα= АВ/ОА, а так как ОА=1рад, то tgα = АВ = mкр дин. Динамический угол крена при известном кренящем моменте определяется абсциссой точки пересечения С графиков работы кренящего и восстанавливающего моментов.
Рис. 28. Определение предельных значений динамического угла крена и динамического кренящего момента.
Для определения предельных величин кренящего момента и угла крена строится график работы максимального кренящего момента, который представляет собой касательную к диаграмме динамической остойчивости, проведенную из начала координат. Абсцисса точки касания Е определяет предельное значение динамического угла крена θдин max, a ордината этой касательной при θ=1рад (отрезок AD) — величину максимального динамического кренящего момента, который может выдержать подводная лодка.
Добавить комментарий